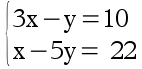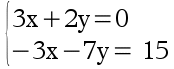Méthode par substitution
a) 3x – y = 10 on peut écrire y = 3x - 10 ou x = (10 + y)/3
x – 5y = 22 x = 22 + 5y ou y = (x – 22)/5
b) Il suffit de remplacer y ou x dans une des expressions à partir de l'autre
c) On peut remplace y par 10 – 3x dans l'égalité x – 5y = 22
x – 5(3x - 10) = 22 on développe x – 5 x 3x + 5 x 10 = 22
on résout x - 15x + 50= 22
- 14x + 50 = 22 -14x = 22 - 50 x = -28/(-14) = 2
d) 3x – y = 10 3 x 2 - y = 10 - y = 10 - 6 - y = 4 y = -4
e) le couple trouvé est (2; - 4) on remplace x par 2 et y par - 4 dans les deux équations
3x – y = 3 x 2 – (- 4) = 6 + 4 = 10 la première équation est vérifiée
x – 5y = 2 – 5 x (- 4) = 2 + 20 = 22 la deuxième équation est vérifiée
le couple (2; - 4) est donc bien solution du système
a)
1ère méthode :
En additionnant les premiers membres des 2 équations on va faire disparaitre l'inconnue x :
3x + 2y + (-3x – 7y) = 3x + 2y - 3x – 7y = - 5y
Cette somme est égale à la somme des 2 seconds termes soit : 0 + 15 = 15
On obtient l'équation à une inconnue : - 5y = 15 soit y = - 15/5 = - 3
Pour trouver x, il suffit d'utiliser une des équations : 3x + 2y = 0
soit 3x + 2x(-3) = 3x - 6 = 0 soit x = 6/3 = 2
le couple (2 ; -3) est donc solution du système
b)
2ème méthode :
Si on veut faire disparaitre l'inconnue y, les coefficients de y doivent être les mêmes. Pour y parvenir il suffit de multiplier la première équation par 7 et la deuxième par 2 pour obtenir 14.
3x + 2y = - 4 7 x(3x + 2y) = 0 x 7 soit 21x + 14y = 0
-3x – 7y = 15 2 x (-3x – 7y) = 2 x 15 soit - 6x – 14y = 30
en
additionnant membre à membre on a :
21x - 6x = 0 – 30 15x =
30 x = 30/15 = 2
Pour trouver y, il suffit d'utiliser une des équations : 3x + 2y = 0
soit 3x2 + 2y = 6 + 2y = 0 soit y = -6/2 = -3
le couple (2 ; -3) est donc solution du système
c) Vérification du couple solution
3x + 2y = 3 x 2 + 2 x (-3) = 6 - 6 = 0
-3x – 7y = -3 x 2 – 7 x (-3) = -6 + 21= 15
les 2 équations sont vérifiées donc le couple (2 ; -3) est bien solution du système