Méthode des soustractions
Exemple : Jean a choisi les nombres 42 et 14
42
= 7
x 6 14 = 7
x 2
7 est
un diviseur
commun à 42 et 14
42
+ 14 = 7 x 6
+ 7 x 2
= 7 x (6 + 2)
= 7 x 8 = 56
7 est
un diviseur de 42 + 14
42
- 14 = 7 x 6
- 7 x 2
= 7 x (6 - 2)
= 7 x 4 = 28
7 est
un diviseur de 42 - 14
Avec
des lettres : Si k est un diviseur commun à a et b.
Compléter
a
= k
x c
b = k
x d
k est un diviseur commun à a et b ainsi que de a - b
Propriété
1 : Un diviseur commun de deux
nombres entiers divise
aussi leur somme ou leur différence
a
et b sont des entiers naturels et a ≥
b, PGCD (a ; b) = PGCD (b ; a – b).
Comment
trouver le PGCD de deux nombres ?
(Méthode
par
soustractions successives)
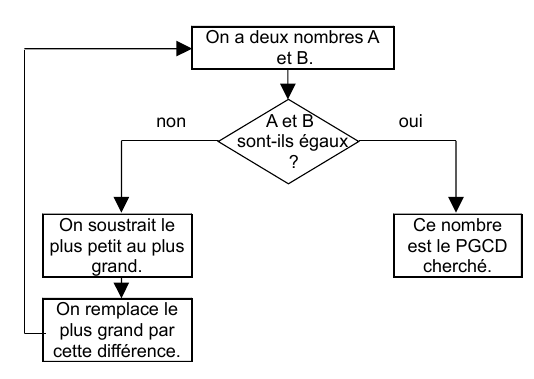
Calculons le PGCD de 936 et 624.
936 – 624 = 312 On calcule la différence des 2 nombres
A chaque étape, on remplace les 2 nombres par le plus petit des 2 et la différence des 2 nombres
624
– 312 = 312
312
– 312 = 0
Le PGCD cherché est la dernière différence non nulle
Le PGCD de 936 et 624 est 312.
Méthode des divisions successives ou algorithme d'Euclide
Exemple: Jean a choisi les nombres 248 et 32 .
248
= 62
x 4
32 = 8 x 4
4 est
un diviseur
commun à 248 et 32
248
= 32 x 7
+ 24
24 est
le reste de la division euclidienne de 248 par 32
24
=
6 x
4
4 est
un diviseur de 32 et du reste de la division de 248 par 32
PGCD( a ; b) = PGCD( b ; r)
Propriété 2 : a et b sont des entiers naturels et a ≥ b, PGCD (a ; b) = PGCD (b ; r) où r est le reste de la division euclidienne de a par b
Comment
trouver le PGCD de deux nombres ? (Algorithme
d'Euclide)

Calculons le PGCD de 180 et 170.
-
PGCD(180 ; 170)
= PGCD(10; 170)
=10
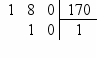
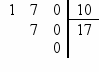
Donc le PGCD de 180 et 170 est 10.
Propriété : 1) Si
a est un diviseur de
b alors PGCD (a ; b) = a
2)
PGCD( a ; a) = a